http://www.qsarworld.com/insilico-chemistry-model-applicability.php
When using a model for predicting the value(s) for some unknown compound(s), assessment of the applicability of the model, in context of the compound(s) under study, is necessary. This can be assessed with different approaches, all of which in some sense try to assess whether the structure-, chemical-, or descriptor-based properties of the ‘unknown’ compound lie in similar ‘space’ as those for the compounds that were part of the training set used for building the model. This is an issue because the basic assumption of QSAR modeling is that similar compounds have similar activity/property and hence, given an unknown compound, we shall be able to predict its activity/property with confidence if it is ‘similar’ to the compounds that were used for building the model.
Whether the compound(s) under study is ‘similar’ to the training set compounds can be assessed in various ways:
1) Structure-based similarity: Tanimoto coefficient values, obtained by comparing MACCS fingerprints, can be used to assess structural similarity. If any of the training set compound has a Tanimoto coefficient value > 0.85 when compared against the compound under study, the same can be taken as an indication of high structural similarity and it can be believed that the given model is applicable for this case.
2)Descriptor-based similarity: Similarity of the compound under study against the compounds in the training set can also be estimated by computing the distances (Euclidean) of the descriptors, that were used in training the model, between the unknown compound(s) and the training set compounds. This distance should lie between 0 to ∞ and possibly, the lesser the distance the better it is.
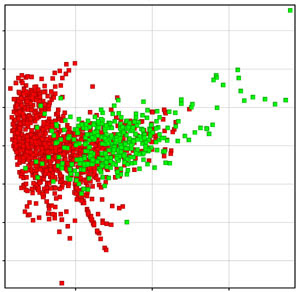
3) Chemical Space: Comparing the ‘chemical space’ of the ‘unknown’ compounds against the compounds in the training set (used for building the model) can be another way to assess model applicability. What can be done here is to run a Principal Components Analysis (PCA) on the descriptors used in the model, for both the training set and the ‘unknown’ compounds, and then launch a plot on the first two components. In the figure below, the training set compounds are shown in red while the ‘unknown’ compounds, for which the predictions need to be made, are depicted in green. Thus, at a glance it can be visualized if the ‘unknown’ compounds belong to the same distribution or ‘space’ as the ones used for deriving the model (and decide for or against using the given model).
4) Statistical Measures: The model can anyway be used for predicting the values for the ‘unknown’ compounds. The predicted values usually also have a measure of statistical significance associated with them.
In case of regression models (prediction of a continuous value), this measure is in terms of standard error. A simple interpretation of the standard error is that, according to the model, the predicted value lies in an interval bound by +/- standard error with a 95% confidence. Say, the predicted value is x and the associated standard error is y, then the value is estimated to lie in x-y to x+y interval with a 95% confidence. (This however does not imply that there exists some interval wherein the confidence could be 100%).
In case of classification models (prediction of a categorical value), the statistical significance is in terms of confidence measure. This lies in a 0-1 scale and can be interpreted as the % confidence that the underlying algorithm (in the model) has when it is predicting some given compound to belong to a particular class. Say, if an ‘unknown’ compound is called by the model to belong to a particular class, and the model associates a confidence measure of 0.90 with that prediction, this implies that the algorithm is 90% confident about making this prediction. In other words, statistically, in the long run, when the algorithm makes large enough such predictions, 90% of them would turn out to be correct.
Entradas
No hay comentarios:
Publicar un comentario